正射影ベクトルは医学部や東大・京大の数学入試の図形問題に頻出です
物体に光が当たるり、その背後に形成される「影」が、私たちの世界に不思議な次元を加えます。
この現象は学術的に「射影」と呼ばれます。
そして、その中でも特別な形態が存在します。
それは、「正射影」と呼ばれるものです。
これはスクリーンに対して垂直に光を投影することで生まれます。
この正射影は、ただの光と影のゲームではありません。
実は、医学部や東大などの難関大学の数学入試では、この正射影を理解し、巧みに利用することで解決の糸口を見つけることができる問題が頻出しています。
この記事では、正射影がどのように数学問題の解決に役立つのか、その魅力とテクニックについて深掘りしていきます。
このワザを実践に落とし込んで成績向上を狙いたい方、より詳しく知りたい方は「鍛錬場」にお問い合わせください。
鍛錬場では、オンライン指導を通じてサポートいたします。
是非とも下記をクリックして、お問い合わせ下さいませ。
鍛錬場の紹介ページはこちらから

目次
正射影ベクトルとは?
正射影ベクトルは数学の中でも特に重要な概念の一つです。
このセクションでは、正射影ベクトルの基本的な理解から始め、その重要性を探ります。
正射影ベクトルの基本概念
正射影ベクトルは、ベクトルの投影として理解されます。

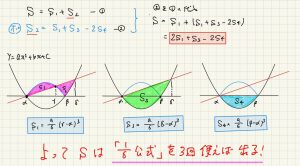
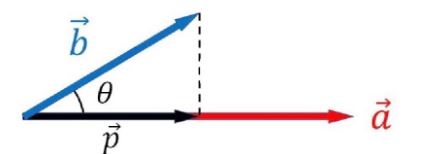
正射影ベクトルとは上の図におけるpです。
bのaへの正射影ベクトルをpと言います。
正射影ベクトルの公式とその証明
正射影ベクトルを計算するための公式と、その公式がなぜ成り立つのかを証明します。

上の式は、その前の図の、ベクトルpを示しています。
これは極めて重要な公式で、非常に役立ちます。
どのように役立つか、以下に書いてゆきます。
正射影ベクトルの応用

正射影ベクトルは、数学入試において頻出のトピックです。
このセクションでは、実際の入試問題での応用例を通じて、その使い方を学びます。
入試問題での正射影ベクトル(2009京大)
以下、2009年の京都大学の問題です。
xyz平面上の2点A(−3,−1,1),B(−1,0,0)を通る直線Lがある。
この直線Lに点C(2,3,3)から下ろした垂線の足Hの座標を求めよ。
正射影ベクトルを用いた解法
点Hの座標を求める
⇒ ベクトルOHを求め、その成分が点Hの座標
⇒ OH=OA+AHより、AHを求めれば良い
⇒ AHは、ABのACに対する「正射影ベクトル」
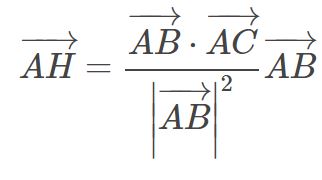
これを用いて計算すると、以下のようになる。
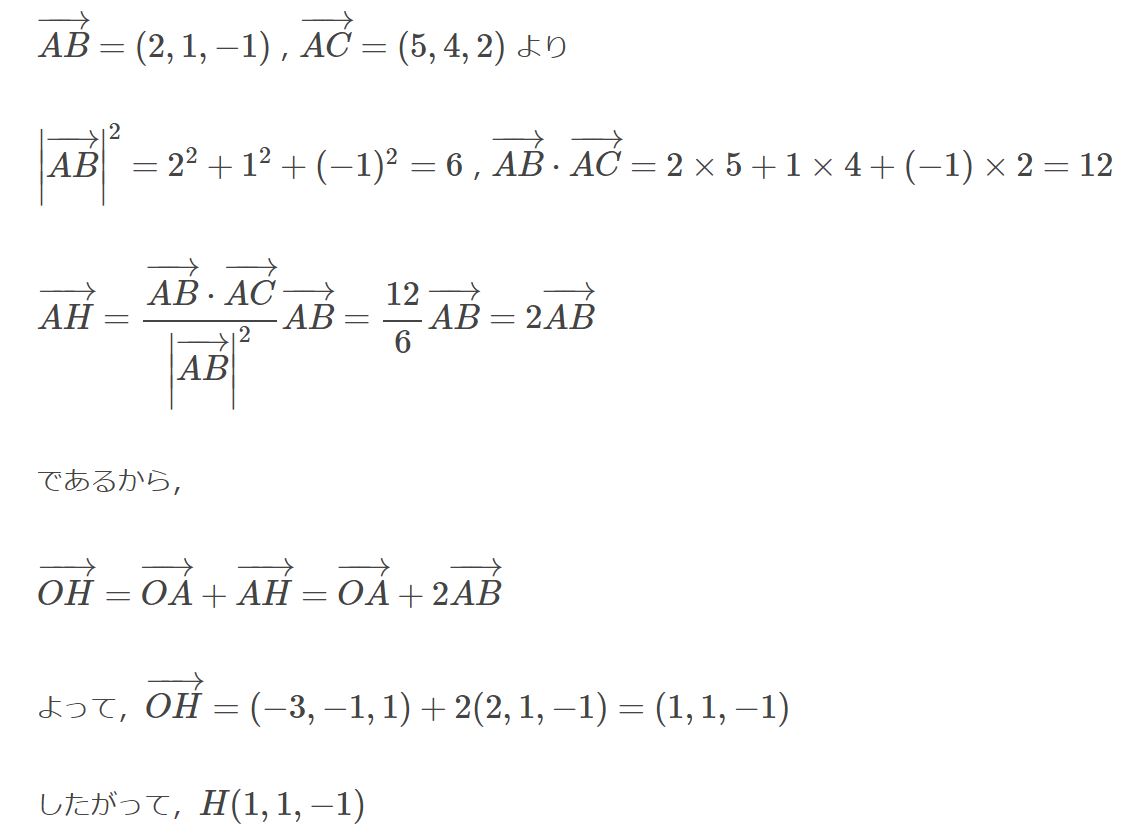
平面への垂線の足
 上記の問題は「空間における1点から直線におろした垂線の足」でした。
上記の問題は「空間における1点から直線におろした垂線の足」でした。
実は「空間における1点から平面におろした垂線の足」という問題にも使えるのです。
それは「外積」とも関係してきます。
次回のブログ記事で書いていきますね。
鍛錬場で頑張ろう!
鍛錬場では、このような幅広いコーチングサービスを提供しています。
ぜひ以下にアクセスして下さい。
鍛錬場の紹介ページはこちらから